Blog of Veikko M.O.T. Nyfors, Hybrid Quantum ICT consultant
Quantum Mechanics demystified, a try
Project maintained by veikkonyfors Hosted on GitHub Pages — Theme by mattgraham
Nabla Operator
Nabla operator, $\nabla$, describes the gradient of a scalar field in multiple dimensions.
It is a mathematical vector operation, widely used in physics, e.g. in connection of Maxwell equations.
In three dimensions, as used in Maxwell equations, operation is as below:
$\nabla f = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right)$
Or
∇f(x,y,z) = (∂f/∂x, ∂f/∂y, ∂f/∂z)
= (f(x+1,y,z)-f(x,y,z), f(x,y+1,z)-f(x,y,z), f(x,y,z+1)-f(x,y,z))
So, if you would have a scalar field like below (in 2 dimensions only, 3 would be harder to present):
| 40 | 60 | 60 | 60 | 60 |
| 60 | 85 | 85 | 85 | 60 |
| 60 | 85 | 100 | 85 | 60 |
| 60 | 65 | 85 | 85 | 60 |
| 60 | 60 | 60 | 60 | 60 |
you would end up having a vector field as follows
| (20,20) | (0,25) | (0,25) | (0,25) | (0,0) |
| (25,0) | (0,0) | (0,15) | (-25,0) | (0,0) |
| (25,22.5) | (15,20.0) | (-15,0.0) | (-25,-20.0) | (0,-22.5) |
| (5,0) | (-20,-5) | (0,-25) | (-25,-25) | (0,0) |
| (-10.0,0) | (-22.5,0) | (-22.5,0) | (-22.5,0) | (-10.0,0) |
As an image
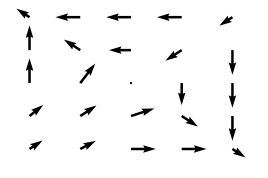
Shortly said, nabla tells into which direction scalar field is changing at each monitored spot.